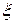Определить сопротивление медного провода двухпроводной линии передачи при t 20

Сопротивление провода.

Данная статья поможет вам рассчитать сопротивление провода. Расчет можно выполнить по формулам, либо по данным таблицы «сопротивление проводов», которая приведена ниже.

То как влияет материал проводника учитывается при помощи удельного сопротивления, которое принято обозначать буквой греческого алфавита ρ и являет собой сопротивление проводника сечением 1 мм 2 и длинной 1 м. У серебра наименьшее удельное сопротивление ρ = 0,016 Ом•мм 2 /м. Ниже приводятся значения удельного сопротивления для нескольких проводников:

• Сопротивление провода для серебра — 0,016,
• Сопротивление провода для свинеца — 0,21,
• Сопротивление провода для меди — 0,017,
• Сопротивление провода для никелина — 0,42,
• Сопротивление провода для люминия — 0,026,
• Сопротивление провода для манганина — 0,42,
• Сопротивление провода для вольфрама — 0,055,
• Сопротивление провода для константана — 0,5,
• Сопротивление провода для цинка — 0,06,
• Сопротивление провода для ртути — 0,96,
• Сопротивление провода для латуни — 0,07,
• Сопротивление провода для нихрома — 1,05,
• Сопротивление провода для стали — 0,1,
• Сопротивление провода для фехрали -1,2,
• Сопротивление провода для бронзы фосфористой — 0,11,
• Сопротивление провода для хромаля — 1,45

Так как в состав сплавов входят разные количества примесей, то удельное сопротивление может изменятся.

Сопротивление провода рассчитывается по формуле,которая приведена ниже:

• R — сопротивление,
• Ом; ρ — удельное сопротивление, (Ом•мм 2 )/м;
• l — длина провода, м;
• s — площадь сечения провода, мм 2 .

Площадь сечения рассчитывается так:

S=(π?d^2)/4=0.78?d^2≈0.8?d^2

Измерить диаметр провода можно микрометром либо штангенциркулем,но если их нету под рукой,то можно плотно намотать на ручку (карандаш) около 20 витков провода, затем измерить длину намотанного провода и разделить на количество витков.

Для определения длинны провода,которая нужна для достижения необходимого сопротивления,можно использовать формулу:

1.Если данные для провода отсутствуют в таблице,то берется некоторое среднее значение.Как пример ,провод из никелина который имеет диаметр 0,18 мм площадь сечения равна приблизительно 0,025 мм2, сопротивление одного метра 18 Ом, а допустимый ток 0,075 А.

2.Данные последнего столбца,для другой плотности тока, необходимо изменить. Например при плотности тока 6 А/мм2, значение необходимо увеличить вдвое.

Пример 1. Давайте найдем сопротивление 30 м медного провода диаметром 0,1 мм.

Решение. С помощью таблицы берем сопротивление 1 м медного провода, которое равно 2,2 Ом. Значит, сопротивление 30 м провода будет R = 30•2,2 = 66 Ом.

Расчет по формулам будет выглядеть так: площадь сечения : s= 0,78•0,12 = 0,0078 мм2. Поскольку удельное сопротивление меди ρ = 0,017 (Ом•мм2)/м, то получим R = 0,017•30/0,0078 = 65,50м.

Пример 2. Сколько провода из манганина у которого диаметр 0,5 мм нужно чтобы изготовить реостат, сопротивлением 40 Ом?

Решение. По таблице выбираем сопротивление 1 м этого провода: R= 2,12 Ом: Чтобы изготовить реостат сопротивлением 40 Ом, нужен провод, длина которого l= 40/2,12=18,9 м.

Расчет по формулам будет выглядеть так. Площадь сечения провода s= 0,78•0,52 = 0,195 мм 2 . Длина провода l = 0,195•40/0,42 = 18,6 м.

Источник

Как вычислить сопротивление проводника

Использование меди в электротехнических устройствах обусловлено двумя факторами: хорошей проводимостью и относительной дешевизной. При проектировании или ремонте линий электропередач или электронных приборов, необходимо учитывать сопротивление медных проводов. Пренебрежение данным параметром приведет к поломке электрической системы.

Что такое сопротивление медного провода

В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.

При прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.

Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.

Важно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству.

Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.

Что влияет на сопротивление медного провода

Электрический импеданс медного кабеля зависит от нескольких факторов:

• Удельного сопротивления;
• Площади сечения проволоки;
• Длины провода;
• Внешней температуры.

Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.

Зависимость сопротивления

Удельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.

Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.

Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20[1+ α(t−20°C)]. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.

Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.

Таблица удельного сопротивления

Согласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.

Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».

Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения.

Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.

Последним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.

Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление.

Как узнать сопротивление 1 метра медного провода

После выяснения всех факторов, влияющих на резистентность медного провода, можно объединить их в формуле зависимости сопротивления от сечения проводника и узнать, как вычислить этот параметр. Математическое выражение выглядит следующим образом: R= pl/s, где:

• ρ — удельное сопротивление;
• l — длина проводника, при нахождении сопротивления медного проводника длиной 1 м, l = 1;
• S— площадь поперечного сечения.

Для вычисления S, в случае провода цилиндрической формы, используется формула: S = π ∙ r2 = π d2/4 ≈ 0.785 ∙ d2, здесь:

• r — радиус сечения провода;
• d — его диаметр.

Если провод состоит из нескольких жил, то суммарная площадь будет равна: S = n d2/1,27, где n — количество жил.

Если проводник имеет прямоугольную форму, то S = a ∙ b, где a — ширина прямоугольника, b — длина.

Важно! Узнать диаметр сечения можно штангенциркулем. Если его нет под рукой, то намотать на любой стержень измеряемую проволоку, посчитать количество витков, желательно, чтобы их было не меньше 10 для большей точности. После этого измерить намотанную часть проводника, и разделить значение на количество витков.

Как правильно рассчитать сопротивление провода по сечению

Проектируя электрическую сеть, необходимо правильно подобрать сечение кабеля, чтобы его резистентность не была высокой. Большой импеданс вызовет падение напряжения выше допустимого значения. В результате подключенное к сети электрическое устройство может не заработать. Также, провода начнут перегреваться.

Для правильного расчета минимального сечения необходимо учесть следующие факторы:

• По стандартам ПУЭ падение напряжения не должно быть больше 5%.
• В бытовых условиях ток проходит по двум проводам. Поэтому, при расчете величину сопротивления нужно умножить на 2.
• Учитывать нужно мощность всех подключенных приборов на линии. Для развития предусмотреть запас по нагрузке.

Как вычислить сопротивление проводника по формуле? Для примера можно рассмотреть задачу. Требуется определить: достаточно ли будет медного кабеля сечением 2,5 мм2 и длиной 30 метров для подключения оборудования мощностью 9 кВт.

Формулы электрической цепи

Задача решается следующим образом:

• Резистентность медного кабеля будет равна:

2 ∙ (ρ ∙ L) / S = 2 ∙ (0,0175 ∙ 30) / 2,5 = 0,42 Ом.

• Для нахождения падения напряжения нужно определить силу тока, по формуле: I= P/U.

Здесь P — суммарная мощность оборудования, U — напряжение в цепи. Тогда сила тока будет равна: I = 9000 / 220 = 40,91 А.

• Используя закон Ома, можно найти падение напряжения по кабелю: ΔU = I ∙ R = 40, 91 ∙ 0,42 = 17,18 В.
• От 220 В процент падения составит: U% = (ΔU / U) ∙ 100% = (17,18 / 220) ∙ 100% = 7, 81%>5%.

Падение напряжение выходит за пределы допустимого значения, значит необходимо использовать кабель большего сечения.

Таблица сопротивления медного провода

Узнать резистентность проводника можно по таблицам. В них содержатся готовые результаты вычислений для разных кабелей.

Например, сопротивление меди на метр для различных сечений можно определить без вычислений, из соответствующей таблицы.

Важно! Таблицы не содержат данные о всех сечениях. Если нужно узнать величину импеданса для неуказанного кабеля, то находится среднее значение между двумя ближайшими известными сопротивлениями.

Расчет сопротивления кабеля является важной задачей при проектировании электрической системы. Воспользовавшись формулами или таблицами, можно успешно ее решить.

Источник

Тема 2. Волноводные линии передач

Антенны и устройства СВЧ. Учебный практикум для студентов специальности 160905 – «Техническая эксплуатация транспортного радиооборудования».

Томск: Томский государственный университет систем управления и радиоэлектроники, 2012. 70 с.

Приведены основные расчетные формулы, примеры решения типовых задач и многовариантные задачи для самостоятельной работы. Рекомендуется использовать решения типовых задач при изучении соответствующих разделов лекционного курса, а многовариантные задания для самостоятельных и контрольных работ. Учебный практикум составлен для студентов специальности 160905, но может быть использован и студентами других специальностей радиотехнического профиля очной, заочной и дистанционной формы обучения.

Ó Кафедра КИПР Томского государственного

университета систем управления и

1 Тема 1. Линии передач в виде проволочных и коаксиальных фидеров…………………………………………. 5

1.1 Основные формулы для расчёта проволочных и коаксиальных фидеров………………………………………………………………….……………5

1.2. Примеры решения типовых задач расчёта проволочных и

1.3 Задачи для самостоятельной работы. 11

2 Тема 2. Волноводные линии передач…………………14

2.1 Краткие сведения по расчету параметров волноводных линий передач ……………………………………………………………………………….14

2.1.1 Расчет параметров прямоугольных волноводов………………….14

2.1.2 Расчет параметров круглых волноводов…………………………..18

2.1.3 Расчет параметров П— и Н— волноводов…………………………..20

2.1.4 Расчет параметров полосковых волноводов…………………….21

2.2 Примеры решения типовых задач…………………………………..25

2.2.1 Примеры решения задач по расчету параметров прямоугольных волноводов……………………………………………………………………. 25

2.2.2 Примеры решения задач по расчету параметров круглых волноводов……………………………………………………………………………..34

2.2.3 Пример решения задачи по расчету параметров П— и Н— волноводов………………………………………………………………………………..42

2.2.4 Примеры решения задач по расчету параметров полосковых волноводов…………………………………………………………………………..42

2.3 Задачи для самостоятельной работы по расчету параметров волноводных линий передач ………………………………………………..………..52

2.3.1 Задачи по расчету параметров прямоугольных волноводов..…..52

2.3.2 Задачи по расчету параметров круглых волноводов………..…..54

2.3.3 Задача по расчету параметров П— и Н— волноводов……….…….55

2.3.4 Задачи по расчету параметров полосковых волноводов…….…56

3 Тема 3. Энергетические соотношения в линииях передач………………………………………………………………………60

3.1Основные формулы для расчёта энергетических соотношений в линиях передач…………………………………………………………….………60

3.2 Примеры решения типовых задач расчёта энергетических соотношений в линиях передач………………………………………………………..62

3.3 Задачи для самостоятельной работы…………………………..……65

СПИСОК рекомендуемой ЛИТЕРАТУРЫ…………………….70

Учебный практикум по курсу «Антенны и устройства СВЧ» содержит разработанные варианты практических занятий, построенных по единому принципу. В каждом его разделе вначале даются краткие теоретические сведения, затем приводятся подробные решения типовых задач и в заключение предлагаются многовариантные задания для самостоятельного решения каждым студентом. Цель данного практикума состоит в оказании помощи студентам в освоении лекционного курса и в выполнении контрольных работ. Так как расчёты антенн достаточно громоздки, то они осваиваются студентами при выполнении курсового проекта. На практических же занятиях студенты решают задачи расчёта устройств СВЧ, используемых в антеннах. В частности, они производят расчёт конструктивных и электрических параметров линий передач, рассчитывают энергетические соотношения в линиях передач и устройства согласования между входом линии передач и нагрузкой.

1 Тема 1. Линии передач в виде проволочных и коаксиальных фидеров

1.1 Основные формулы для расчёта проволочных и коаксиальных фидеров

Линия передачи (ЛП) – это устройство, ограничивающее область распространения электромагнитных колебаний и направляющее поток электромагнитной энергии к нагрузке. В этом разделе будут рассмотрены только однородные, регулярные ЛП. Однородные ЛП заполнены однородной средой, а в регулярных ЛП в продольном направлении неизменны поперечное сечение и свойства среды [1]. Для передачи энергии в диапазонах длинных, средних, коротких и отчасти дециметровых волн применяют проволочные фидеры, а в диапазоне СВЧ закрытые и открытые волноводы.

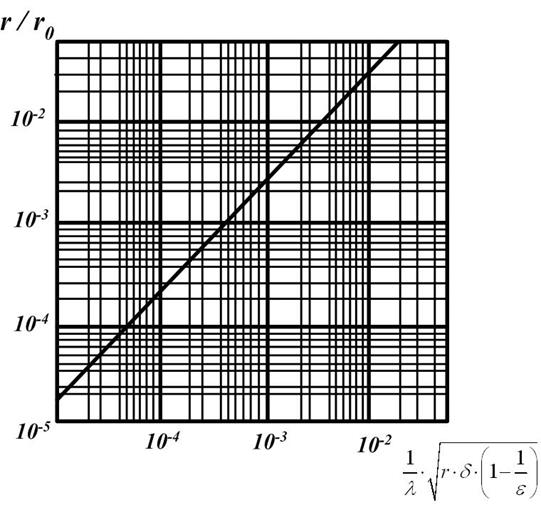
В данном разделе рассмотрены ЛП в виде проволочных и коаксиальных фидеров. Эти ЛП характеризуются следующими параметрами: волновым сопротивлением Wop, активным погонным сопротивлением R₁, погонными ёмкостью C₁ и индуктивностью L₁. Расчёт параметров для некоторых типов фидеров, выполненных из меди, можно проводить по формулам таблиц 1.1 и 1.21 [2]. Буквенные обозначения в этих формулах: ε— относительная диэлектрическая проницаемость диэлектрика, используемого в фидере, l — длина волны, м, r₀ – предельный радиус, определяемый из графика (рисунок 1.1), приведенного в [2]. Все размеры при использовании графика должны подставляться в мм.

Длина волны в фидере l_ф, распространяющейся вдоль однопроводного фидера определяется по формуле

. (1.1)

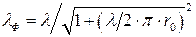
Значения r и а в формулы для определения R₁ подставляются в мм. Затухание a (дБ/м) рассчитывают по формуле

, (1.2)

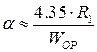
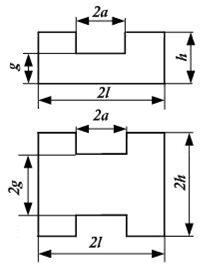
а коэффициент укорочения волны в фидере (кроме однопроводного) по формуле

. (1.3)

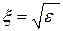
В коаксиальном фидере из произвольного металла, заполненным диэлектриком с углом диэлектрических потерь tgd, затухание a (дБ/м) рассчитывают по формуле [1, 5]

, (1.4)

, (1.5)

, (1.6)

, , (1.7)

, , (1.8)

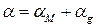
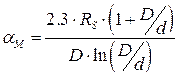
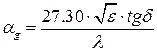
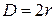
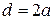
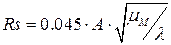
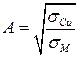
m_м – относительная магнитная проницаемость металла,

А – коэффициент, учитывающий отличие проводимости металла проводника s_М от проводимости меди s_Сu (для меди А=1, для серебра 0,98, для алюминия 1,35, для золота 1,2); длина волны l берется в м.

Рисунок 1.1 –График дляопределения отношения радиуса провода

r однопроводногофидера, покрытого диэлектриком к

Предельная мощность Р_пр, передаваемая по коаксиальному фидеру бегущей волной :

Таблица 1.1- Формулы для расчёта параметров однопроводного фидера, покрытого диэлектриком, и для двухпроводного фидера [2]

Параметр	Тип фидера
Однопроводнойфидер, покрытый диэлектриком	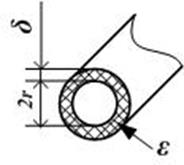Двухпроводной фидер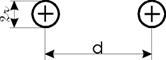
Ёмкость С1 пФ/м Индуктивность L1 , мкГн/м Сопротивление R1 , Ом/м Волновое сопротивление WФ, Ом	— —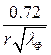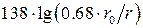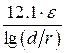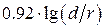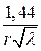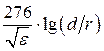

Параметр	Тип фидера
Четырёхпроводный перекрещенный фидер	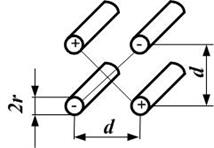Коаксиальный фидер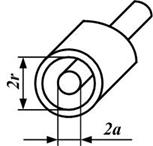
Ёмкость С1 пФ/м Индуктивность L1 , мкГн/м Сопротивление R1 , Ом/м Волновое сопротивление WФ, Ом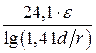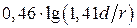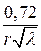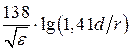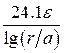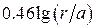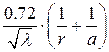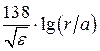

Таблица 1.2- Формулы для расчёта параметров четырёхроводного перекрещенного фидера и для коаксиального фидера [2]

Примечание: Если в четырех проводной линии синфазными являются провода, лежащие по одну сторону от вертикали, то в приведенных формулах сомножитель 1,41 под знаком lg следует перенести из числителя в знаменатель [2]

, (1.9)

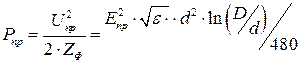
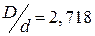
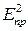
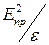
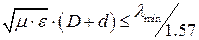
где Е_пр – предельная пробивная прочность диэлектрика (для сухого воздуха Е_пр » 30 кВ/см); U_np – пробивное напряжение. Максимум пробивного напряжения соответствует (Z_Ф=60 Ом), максимум Е_пр при (D/d )=1,65 (Z_Ф = 30 Ом), а минимум затухания в металле при (D/d)=3,6 (Z_Ф=77 Ом). Стандартные гибкие коаксиальные кабели имеют Z_Ф равные 50, 75, 100 или 200 Ом. Их эксплуатационные характеристики описаны в [3]. В [4] рекомендуют при расчете Р_пр при сплошном заполнении диэлектрика делать запас и в формуле (1,9) вместо представлять значение ( ). Для линий с металлическими изоляторами Е_пр занижают при расчете Р_пр в 6-7 раз, а в коаксиалах с диэлектрическими изоляторами в 15-20 раз [3]. Чтобы не возникло паразитных типов волн должно соблюдаться условие [4,7]

, (1.10)

где l_min – минимальная длина волны рабочего диапазона, m — относительная магнитная проницаемость диэлектрика.

1.2. Примеры решения типовых задач расчёта проволочных и коаксиальных фидеров

1.2.1.Двухпроводный медный фидер имеет волновое со­противление W_Ф, = 300Ом. Погонная индуктивность фидера L₁ = 2 мкГн/м. Определить относительную диэлектриче­скую проницаемость диэлектрика, используемого в фидере. Чему равен коэффициент укорочения волны в таком фидере?

1. Волновое сопротивление W_Ф двухпроводной воздушной (ε=1) линии передачи равно

индуктивность двухпроводной линии передачи равна

L₁ = 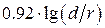,мкГн/м.

а коэффициент укорочения волны в фидере (кроме однопроводного) равен

.

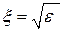
2.Отсюда находим коэффициент укорочения волны в фидере

= L₁ / 0,92= W_Ф ,

=276 L₁ / (0,92 W_Ф) =276∙2 / (0,92 ∙300) = 2,

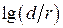
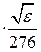
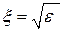
а затем и относительную диэлектриче­скую проницаемость диэлектрика

= 4.

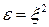
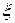
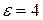
Ответ: коэффициент укорочения волны =2, а относительная диэлектриче­ская проницаемость диэлектрика . (зад. 4.2)

1.2.2 Определить параметры коаксиального медного фидера с полиэтиленовой ( 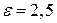) изоляцией, размеры которого 2r = 24 мм,2а= 6 мм. Длина рабочей волны l = 30 м.

1.Определим погонную ёмкость С₁, пФ/м:

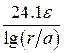
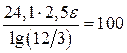
С₁ = = пФ/м.

2.Определим погонную индуктивность L₁ , мкГн/м:

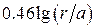
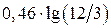
L₁ = = = 0,277 мкГн/м.

3. Определим погонное сопротивление R₁ , Ом/м

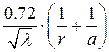
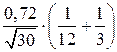
R₁ = = =0,0547 Ом/м.

4. Определим волновое сопротивление W_Ф:

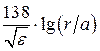
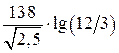
W_Ф= = =52,6 Ом.

Ответ: погонная ёмкость С₁=100 пФ/м, погонная индуктивность L₁ = 0,277 мкГн/м, погонное сопротивление R₁=0,0547 Ом/м, волновое сопротивление W_Ф =52,6 Ом.

1.2.3. Определить затухание в однопроводном медном фидере, покрытом слоем полиэтилена (ε =2,3) толщиной δ = 5 мм, при диаметре провода 2r = 4 мм и длине волны l = 40 cм, если длийа фидера l= 1 км.

1. Определим вспомогательную величину

.

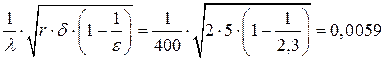
Из графика на рисунке 1.1 находим отношение r / r₀ ≈ 2 ∙ 10 — 2 , откуда предельный радиус r₀ = r /2 ∙ 10 — 2 = 2 /0,02 =100 мм = 10 см.

2. Волновое сопротивление W_Ф провода, по­крытого слоем полиэтилена

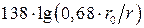
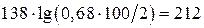
W_Ф = = Ом.

3. По формуле (1.1) определяем длину волны, распространя­ющейся вдоль фидера:

см.

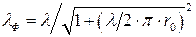
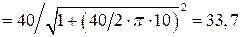
4. По формулам (1.2) и таблицы 1.1 рассчитываем коэффициент за­тухания фидера

дБ/м.

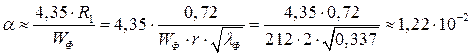
5. Рассчитываем за­тухание в фидере длиной 1 км:

a∙ l = 1,22 ∙ 10 — 2 ∙ 10 3 = 12,2 дБ.

Ответ: затухание в однопроводном медном фидере длиной 1 км равно12,2 дБ.

1.2.4. Определить параметры четырехпроводного перекре­щенного воздушного (ε = 1) фидера, выполненного из мед­ных проводов диаметром 2r = 4 мм. Расстояние между проводами d = 4 см, рабочая длина волны l = 100 м.

1.Определим погонную ёмкость С₁, пФ/м:

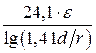
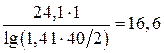
С₁ = = пФ/м.

2.Определим погонную индуктивность L₁ , мкГн/м:

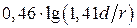
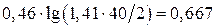
L₁ = = мкГн/м.

3. Определим погонное сопротивление R₁ , Ом/м

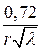
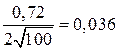
R₁ = = Ом/м.

4. Определим волновое сопротивление W_Ф:

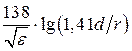
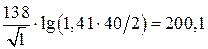
W_Ф= = Ом.

Ответ: погонная ёмкость С₁=16,6 пФ/м, погонная индуктивность L₁ = 0,667 мкГн/м, погонное сопротивление R₁=0,036 Ом/м, волновое сопротивление W_Ф =200,1 Ом.

1.3. Задачи для самостоятельной работы

1.3.1. Определить параметры двухпроводного воздушного (ε = 1) фидера, выполненного из медных проводов диамет­ром 2r мм. Расстояние между проводами d см, рабочая частота f Мгц. Вариант задания для этой задачи назначается преподавателем, и состоит из трёх цифр. Ниже приведена таблица 1.3 с исходными данными согласно варианту задания.

Первая цифра номера варианта
2r, мм	5,5	3,5	5,2	4,2
Вторая цифра номера варианта
d, см
Третья цифра номера варианта
f, Мгц

1.3.2. Четырехпроводный перекрещенный медный фидер имеет данные: волновое сопротивление W_Ф Ом, по­гонная емкость С₁ пФ/м. Предполагая, что потери в фидере отсутствуют, определить диаметр проводов фидера и относительную диэлектрическую проницаемость его ди­электрика, если расстояние между проводами фидера d см. Чему равен коэффициент укорочения волны в та­ком фидере? Вариант задания для этой задачи назначается преподавателем, и состоит из трёх цифр. Ниже приведена таблица 1.4 с исходными данными согласно варианту задания.

Первая цифра номера варианта
WФ, Ом
Вторая цифра номера варианта
С1, пФ/м
Третья цифра номера варианта
d, см	1,8	2,0	2,2	1,7	2,4	1,9	2,1	2,3	2,5	2,7

1.3.3. Коаксиальный медный фидер с твердым диэлект­риком имеет данные: наружный диаметр диэлектрика 2r мм, волновое сопротивление W_Ф, Ом, погонная емкость С₁, пФ/м. Предполагая, что потери в фидере отсутствуют, определить погонную индуктивность, диаметр внутреннего проводника и относительную диэлектрическую проницаемость диэлектрика, используемого в фидереВариант задания для этой задачи назначается преподавателем, и состоит из трёх цифр. Ниже приведена таблица 1.5 с исходными данными согласно варианту задания.

Первая цифра номера варианта

WФ, Ом

Вторая цифра номера варианта

С1, пФ/м

Третья цифра номера варианта

2r, мм

1.3.4. Определить волновое сопротивление, погонное активное сопротивление и коэффициент затухания однопроводного медного фидера, покрытого слоем диэлектрика с относительной диэлектрической проницаемостью ε толщиной δ см, при диаметре провода 2r, мм и длине волны λ м.Вариант задания для этой задачи назначается преподавателем, и состоит из трёх цифр. Ниже приведена таблица 1.6 с исходными данными согласно варианту задания.

Первая цифра номера варианта
ε	2,45	2,5	2,8	3,5	3,4	3,5	3,75	3,7	3,65
δ, см	1,45	1,5	0,8	1,3	1,35	1,4	0,9	0,75	0,7	0,65
Вторая цифра номера варианта
λ, м	1,4	0,9	0,75	0,7	0,65	1,45	1,5	0,8	1,3	1,35
Третья цифра номера варианта
2r, мм	1,8	2,0	2,2	1,7	2,4	1,9	2,1	2,3	2,5	2,7

Тема 2. Волноводные линии передач

2.1 Краткие сведения по расчету параметров волноводных линий передач

2.1.1 Расчет параметров прямоугольных волноводов

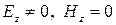
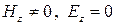
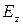
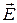
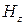
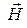
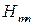
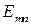
Для волны типа Е в волноводах , а для волны типа Н, . Здесь — это величина проекции напряжённости электрического поля на продольную ось волновода z, совпадающую с направлением распространения энергии, а — величина проекции напряжённости магнитного поля на ось z. Для волн типа и прямоугольных волноводов т и п— целые числа, т — число стоячих полуволн вдоль широкой стенки волновода а, а п — вдоль узкой стенки b.

Критическая (наибольшая) длина волны l_кр для волновода с воздушным заполнением

. (2.1)

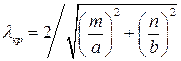
В этом разделе более подробно рассмотрим формулы для инженерного расчета параметров прямоугольных волноводных линии передач на основном типе волны H_min=H₁₀ , имеющем наибольшую величину .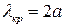

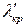
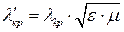
Если же волновод заполнен диэлектриком, то критическая длина волны равна [3]:

, (2.2)

где ε и μ— относительные диэлектрическая и магнитная проницаемости диэлектрика.

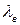
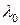
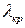
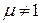
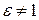
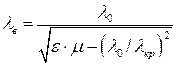
Длина волны в волноводе , длина волны генератора и для и связаны соотношением

. (2.3)

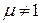
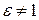
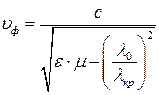
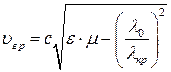
Запишем выражения для фазовой и для групповой скоростей для и :

, (2.4)

. (2.5)

На любой рабочей частоте имеет место соотношение

. (2.6)

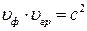
Для волновода с воздушным заполнением

, (2.7)

. (2.8)

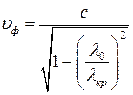
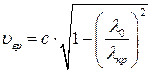
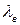
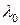
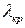
Формулы для , и одинаковы для Е и для Н- волн.

Для волновода с воздушным заполнением критическая частота равна

. (2.9)

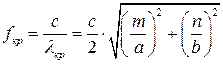
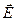
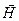
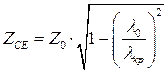
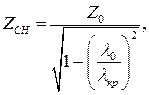
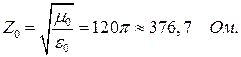
Характеристическое сопротивление волновода это отношение поперечных составляющих векторов и . Для волновода с воздушным заполнением характеристические сопротивления для Е- волн.

, (2.10)

(2.11)

(2.12)

Для волновода с диэлектрическим заполнением характеристические сопротивления для Е- волн

, (2.13)

. (2.14)

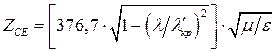
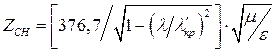
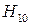
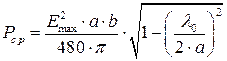
Мощность, переносимая по прямоугольному волноводу с воздушным заполнением волной типа будет

. (2.15)

Здесь Е_тах — амплитуда напряжённости электрического поля.

Наиболее широкополосным, в отсутствии паразитных типов волн, волновод, будет при b£ 0,5а [4]. С другой стороны, при уменьшении b уменьшится предельная мощность P_np , передаваемая по волноводу. Поэтому в стандартных волноводах обычно b=0,5a, а в нестандартных при малой передаваемой мощности можно выбирать b£0,5a.

Предельная мощность, переносимая бегущей волной типа Н₁₀ [3, 5, 6]:

, (2.16)

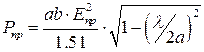
где l, а и b в см, Е_пр – предельная пробивная прочность диэлектрика в кВ/см (для сухого воздуха Е_пр»30 кВ/см), Р_пр предельная пробивная мощность в кВт. Влияние температуры давления газов внутри волновода на предельную мощность Р_{пр Н} [3, 6] описывается выражением

, (2.17)

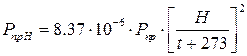
где Р_пр предельная мощность при нормальном давлении Н=101,3×10 3 Па и температуре t = 20°С. Р_прН – эта же мощность при значениях t и Н (Н> 50×10 3 Па) отличных от нормальных.

Коэффициент запаса при определении рабочей мощности Р_раб берут равным от 3 до 5 [6], так как при коэффициенте бегущей волны К меньше единицы предельная переносимая мощность уменьшится:

, (2.18)

. (2.19)

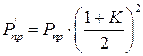
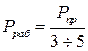
В радиотехнике погонные потери Δ_ПОГ измеряют в дБ на единицу длины. Для прямоугольного волновода с воздушным заполнением на волне основного типа Н₁₀ погонные потери Δ_ПОГ (дБ/м) равны[6]:

Δ_ПОГ= 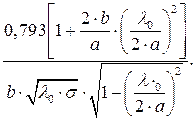(2.20)

Здесь s — удельная электропроводность внутренней поверхности волноводной трубы (См/м).

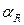
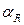
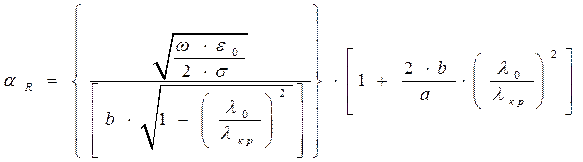
В технике связи погонные потери измеряют в Нп на единицу длины. Для прямоугольного волновода с воздушным заполнением коэффициент затухания (Нп/м) для волн типа Н₁₀ и Н₂₀ равен:

(2.21)

Переход от 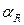к Δ_ПОГ осуществляют с помощью формулы

Δ_ПОГ =8,868∙ 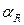. (2.22)

Рабочий диапазон длин волн рассчитывается из условия использования волны Н₁₀ и равномерностей диэлектрических характеристик [3]:

. (2.23)

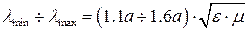
Зависимость скорости распространения волн от частоты (дисперсия) вызывает искажения импульсов в волноводе. Большая часть энергии импульса длительностью τ лежит в полосе частот от f₁ до f₂:

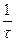
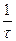
f₁= f₀ — ; (2.24) f₂= f₀ + . (2.25)

При этом групповое время запаздывания Δt волн в волноводе на пути l можно оценить по формуле

Δt(l)= 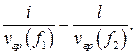(2.26)

2.1.2 Расчет параметров круглых волноводов

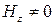
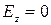
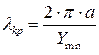
Для волн типа Н_mn ( , ) в круглом волноводе с воздушным заполнением критическая длина волны находится из формулы [7]

, (2.27)

где Y_{m n}— значение n-го корня функции Бесселя J_m(x), а – внутренний радиус волноводной трубы. Значения 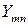приведены в таблице 2.1.

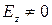
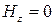
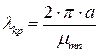
Для волн типа Е_mn ( , ) в круглом волноводе [7] с воздушным заполнением

, (2.28)

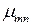
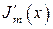
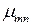
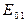
где — значение n-го корня производной от функции Бесселя . Значения приведены в таблице 2.2. Основным типом волны Е является волна .

Таблица 2.1- Корни 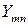Таблица 2.2- Корни

функции Бесселя 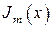производной от функции

Бесселя

n	m=0	m=1	m=2	m=3	m=4
1	3,832	1,841	3,052	4,201	5,318
2	7,016	5,335	6,705	8,016	9,283
3	10,174	8,536	9,965	—	—

n	m=0	m=1	m=2
1	2,405	3,832	5,135
2	5,720	7,016	8,417
3	8,654	10,174	11,62

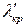
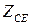
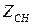
Для основного типа Н волны Н₁₁ с наибольшей критической длина волны l_кр =3,41∙ а, для ближайшего к основному типу волны Е₀₁ — l_{к р} =2,61∙ а ,для Н₂₁ — l_кр=2,06∙ а, а для типов Е₁₁ и Н₀₁ — l_кр=1,64∙ а [3]. Длина волны в круглом волноводе l_В находится по формуле (1.14), по формуле (1.13), характеристические сопротивления по формуле (1.21), а по формуле (1.22). Выражения для фазовой и для групповой скоростей для круглых и прямоугольных волноводов совпадают.

Предельная мощность, переносимая в круглом волноводе бегущей волной основного типа Н волны Н₁₁ [3, 6]

, (2.29)

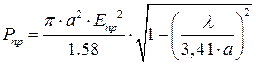
где а, l и l_КР в см, Е_ПР в кВ/см, а Р_ПР в кВт. При коэффициенте бегущей волны К 2 , у волны Е₀₁=505 кВт/см 2 , а у волны Н₀₁=401 кВт/см 2 . Поэтому при больших мощностях во вращающихся сочленениях используют волну Е₀₁. Наименьшим же погонным затуханием (дБ/м) обладает волна Н₀₁. Погонные потери Δ_ПОГ (дБ/м) на волне основного типа Н₁₁ для круглого волновода с воздушным заполнением [3, 6].

, (2.31)

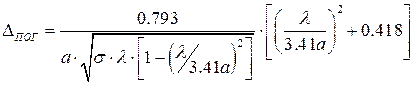
где все линейные размеры измеряются в м, как и в формулах (1.42) и (1.42 а).

, (2.32)

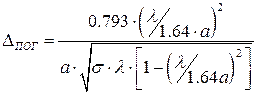
Она не возбуждает в стенках токов, текущих вдоль продольной координаты и её затухание неограниченно уменьшается по мере увеличения частоты эта волна используется в линиях передач для дальней волноводной связи [3, 6].

((2.33)

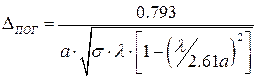
2.1.3 Расчет параметров П— и Н— волноводов

П— и Н — волноводы представляют собой прямоугольные волноводы с одним или двумя выступами и изображены на рисунке 2.1.

Рисунок 2.1 – П и Н волноводы

При тех же габаритных размерах они имеют большую критическую волну основного типа Н₁₀ чем прямоугольные волноводы, в то время как критическая длина волны высшего типа Н₂₀ изменяется мало. Рабочий диапазон частот П— и Н— волноводов, по этой причине, значительно шире чем у прямоугольных, а габариты меньше [3,7]. Если соотношение размеров П— и Н— волноводов соответствует рисунку 1.1, то критические частоты у них одинаковы, волновое сопротивление и коэффициент затухания у Н-волноводов вдвое меньше чем у П— волновода [6]. Коэффициент затухания П— и Н— волноводов больше чем у прямоугольных волноводов. П— и Н— волноводы имеют более плавную зависимость волнового сопротивления от частоты по сравнению с прямоугольными волноводами, что облегчает задачу широкополосного согласования. Меняя высоту гребней можно получить достаточно низкое волновое сопротивление равное волновому сопротивлению коаксиальных линий (50 или 75 Ом). Расчёты волнового сопротивления, коэффициента затухания и предельной мощности проводятся по громоздким формулам, приведённым в [3]. Нами они не рассматриваются. Целесообразно размеры П— и Н-волноводов выбирать следующим образом [3]:

размер 2l выбирать на 20% меньше самой короткой длины волны рабочего диапазона l_min это обеспечивает минимальные габариты при условии, что волновод остается одноволновым

минимальные потери и максимальная пропускаемая мощ

Источник